Smoothing Spline Formulation

Definition

The package implements cubic smooting spline algorithm proposed by Carl de Boor in his book “A Practical Guide to Splines” [1].

The smoothing spline \(f\) minimizes

\[p\sum_{j=1}^{n}w_j|y_j - f(x_j)|^2 + (1 - p)\int\lambda(t)|D^2f(t)|^2dt\]

where the first term is error measure and the second term is roughness measure. Error measure weights \(w_j\) are equal to 1 by default. \(D^2f\) denotes the second derivative of the function \(f\).

The smoothing parameter \(p\) should be in range \([0, 1]\) where bounds are:

  • 0: The smoothing spline is the least-squares straight line fit to the data

  • 1: The natural cubic spline interpolant

The smoothing parameter p can be computed automatically based on the given data sites \(x\).

Note

The calculation of the smoothing spline requires the solution of a linear system whose coefficient matrix has the form \(pA + (1 - p)B\), with the matrices \(A\) and \(B\) depending on the data sites \(X\). The automatically computed smoothing parameter makes p*trace(A) equal (1 - p)*trace(B).

Implementation

csaps is implemented as a pure (without C-extensions) Python modified port of MATLAB CSAPS function that is an implementation of Fortran routine SMOOTH from PGS (originally written by Carl de Boor). The implementation based on linear algebra routines and uses NumPy and sparse matrices from SciPy.

Differences from smoothing splines in SciPy

scipy.interpolate package contains the following classes:

These splines can be computed as \(k\)-ordered (0-5) spline and its smoothing parameter \(s\) specifies the number of knots by specifying a smoothing condition. Also it is only univariate and rect bivariate (2D grid) splines. The algrorithm cannot be used for vectorized computing splines for multivariate and nd-grid cases.

Also the performance of these splines depends on the data size and smoothing parameter s because the number of knots will be iterative increased until the smoothing condition is satisfied:

sum((w[i] * (y[i]-spl(x[i])))**2, axis=0) <= s

Unlike these splines the performance of csaps algorithm only depends on the data size and the data dimension.

csaps spline is cubic only and it has natural boundary condition type. The computation algorithm is vectorized to compute splines for multivariate/gridded data. The smoothing parameter \(p\) determines the weighted sum of terms and limited by the range \([0, 1]\). This is more convenient in practice to control smoothing.

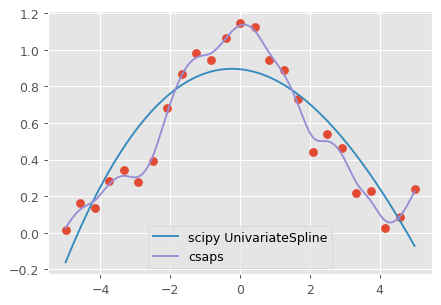
It is an example plot of comparison csaps and scipy.UnivariateSpline (k=3) with defaults (auto smoothing):

_images/formulation-1.png

Footnotes